2020.05.08 在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例:
1 2 3 4 5 6 7 8 输入: 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 输出: 4
又是看题解看的懂,自己就是写不出。。
好吧,唔,服气。
爆破是可以的,但是懒得看。
直接dp解决吧。emmm,具体思想我觉得关键在动态规划方程
直接看代码吧
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Solution {public : int maximalSquare (vector<vector<char >>& matrix) if (matrix.size () == 0 || matrix[0 ].size () == 0 ) return 0 ; int row = matrix.size (); int col = matrix[0 ].size (); int maxsize = 0 ; vector<vector<int >> dp (row,vector <int >(col)); for (int i=0 ;i<row;i++){ for (int j = 0 ;j<col;j++){ if (matrix[i][j]=='1' ){ if (i==0 || j==0 ) dp[i][j]=1 ; else { dp[i][j]=min (min (dp[i-1 ][j],dp[i-1 ][j-1 ]),dp[i][j-1 ])+1 ; } } maxsize = max (maxsize,dp[i][j]); } } return maxsize*maxsize; } };
2020.05.09 今天的题目太简单了。。没什么意思就不写在这里
——就是手写平方根
2020.05.10 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
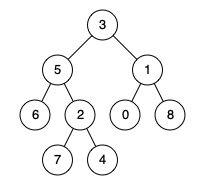
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
今天的题目 有意思
有两种解法。但是不是很想写,就写写第一种吧
递归处理 首先 我们这个函数的功能是:找到在此根节点下的父节点
那么就有几种情况出现
1、此根节点为某一个值——最大父节点为这个
2、此根节点为空——返回空
3、获取左右节点 如果左右节点都是空 说明左子树右子树都没有我们的那两个值
4、左右节点某一支为空,某一支不为空。为空说明该子数没有发现它
5、最后 两个子树都不为空 那么返回本根节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution {public : TreeNode* lowestCommonAncestor (TreeNode* root, TreeNode* p, TreeNode* q) { if (root == NULL ){ return NULL ; } if (root == q || root == p){ return root; } TreeNode * left1 = lowestCommonAncestor (root->left,p,q); TreeNode * right1 = lowestCommonAncestor (root->right,p,q); if (left1==NULL && right1 == NULL ){ return NULL ; } if (left1 == NULL ) return right1; if (right1 == NULL ) return left1; return root; } };
2020.05.11 实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10
输入: 2.10000, 3
输入: 2.00000, -2
-100.0 < x < 100.0
这道题目 核心就是快速幂
相当于从5的56次方——我们求5的28次方——求5的14次方——求5的7次方——求5的3次方——求5的1次方——求5的0次方。
只需要7次就可以得到值。
但是注意到,在我们除二的时候,需要判断此时的幂是否为偶数。、
那么直接代码出来看看
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : double myPow (double x, int n) if (n == 0 ) return 1 ; return solve (x,(long long )n); } double solve (double x,long long n) if (n==0 ) return 1 ; bool right = true ; if (n<0 ){ right = false ; n=-1 *n; } double temp = solve (x,n/2 ); double res = n%2 ==0 ?temp*temp:temp*temp*x; if (right) return res; else return 1.0 /res; } };
2020.05.13 给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
3
/
[
解析——标准地BFS遍历
常见地BFS一般是使用队列来实现
我觉得看代码就懂了!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution {public : vector<vector<int >> levelOrder (TreeNode* root) { vector<vector<int >> ves; queue<TreeNode*> que; if (root == NULL ) return ves; que.push (root); while (!que.empty ()){ vector<int > cenves; int length = que.size (); for (int i=0 ;i<length;i++){ TreeNode * node = que.front (); que.pop (); cenves.push_back (node->val); if (node->left!=NULL ){ que.push (node->left); } if (node->right!=NULL ){ que.push (node->right); } } ves.push_back (cenves); } return ves; } };
2020.05.14 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输入: [4,1,2,1,2]
很像是前面做过的那道题——数组中数字出现的次数
所以很容易想到异或
说明下异或的操作
任何数字和0异或都为原来的值
相同数字异或为0
那么直接可以写出代码了
【再想想还有什么方法:利用map也可以不过需要空间还要时间。
代码如下
1 2 3 4 5 6 7 8 9 10 11 class Solution {public : int singleNumber (vector<int >& nums) int res = 0 ; for (int i=0 ;i<nums.size ();i++){ res=res^nums[i]; } return res; } };
时间复杂度:遍历了一遍数组 故而 O(n)
空间复杂度:没有额外的空间 故而O(1)
2020.05.15 给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2
数组的长度为 [1, 20,000]。
这道题目是有正数有负数。
本来我一开始想的是利用前缀和+尺取法搞定
想一想 一开始觉得很对结果…
nums = 1 1 1 -1 2 这里的k=2
如果按照尺取法,那么在nums[2]的时候 大于2,这个时候l就要加一
那么就不会出现 我们的数组为[1 1 1 -1] = 2这种情况啦
所以尺取法行不通。看了下 尺取法一般用来解决具有单调性的区间问题
下面说说正规的方法:
暴力 i j嘛。我们直接循环查找。
首先最外层i循环 内部 j循环 如果==k,那么就count++
那么代码就有了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : int subarraySum (vector<int >& nums, int k) int count = 0 ; int size = nums.size (); for (int i=0 ;i<size;i++){ int sum =0 ; for (int j=i;j<size;j++){ sum += nums[j]; if (sum == k){ count++; } } } return count; } };
这样极度容易超时。
反省了一下,以后用int size = nums.size()
这样可以节省时间,更加有效。
前缀和+哈希表优化 这个的思路是什么呢?
利用前缀和+map
前缀和在遍历的时候+
因为 sum[j] - sum[i-1] == k 说明 j-i满足和为k的数组
那么在遍历前缀和的时候, 如果 sum[j] - k 存在这个数字
那么我们加上这个数字出现的次数 在这个区间内 有
但是记住 我们是统计 在j这个之前的是否存在 sum[j]-k!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : int subarraySum (vector<int >& nums, int k) map<int ,int > mp; mp[0 ]=1 ; int count = 0 ; int pre = 0 ; for (int i:nums){ pre += i; if (mp.count (pre - k)){ count += mp[(pre-k)]; } mp[pre]++; } return count; } };
我打算之后写写Java的题解,相当于练习java了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int subarraySum (int [] nums, int k) { int pre = 0 ; int count = 0 ; HashMap<Integer,Integer> mp = new HashMap <>(); mp.put(0 ,1 ); for (int i:nums){ pre+=i; if (mp.containsKey(pre - k)){ count+=mp.get(pre - k); } mp.put(pre,mp.getOrDefault(pre, 0 )+1 ); } return count; } }
2020.05.16 给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
示例:
给你这个链表:1->2->3->4->5
当 k = 2 时,应当返回: 2->1->4->3->5
当 k = 3 时,应当返回: 3->2->1->4->5
说明:
你的算法只能使用常数的额外空间。
首先 这题反转链表很简单,但是后面就好难好难
我觉得这道题目 题解解释的很清楚,但是记录下一些很好的东西。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 class Solution {public : ListNode* reverseKGroup (ListNode* head, int k) { ListNode * bhead = new ListNode (0 ); bhead->next = head; ListNode * pre = bhead; while (head){ ListNode * tail = pre; for (int i=0 ;i<k;i++){ tail = tail->next; if (tail == NULL ) return bhead->next; } ListNode * tail_nex = tail->next; tie (head,tail) = rev (head,tail); pre->next = head; tail->next=tail_nex; head=tail_nex; pre=tail; } return bhead->next; } pair<ListNode* ,ListNode* > rev (ListNode* head,ListNode* tail) { ListNode * pre = NULL ; ListNode* cul = head; while (pre != tail){ ListNode* temp = cul->next; cul->next = pre; pre = cul; cul = temp; } return {tail,head}; } };
说实话,我不知道怎么总结这道题目。。 就很无奈。【哎