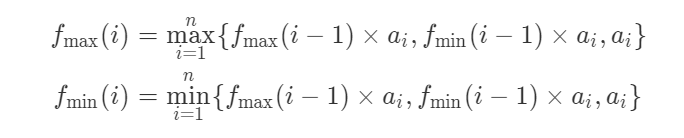前言
21天打卡任务 开始了
2020.05.18
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
强势暴力破解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int maxProduct(vector<int>& nums) {
int ans = 1;
int max_res = INT_MIN;
for(int i=0;i<nums.size();i++){
for(int j = i;j<nums.size();j++){
ans*=nums[j];
max_res = max(ans,max_res);
}
ans = 1;
}
return max_res;
}
};
|
很不幸,超时了。。
动态规划
这个 需要求出动态规划方程
![image]()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
int maxProduct(vector<int>& nums) {
int max_F = nums[0];
int min_F = nums[0];
int ans = max_F;
for(int i = 1;i<nums.size();i++){
int F_max = max_F;
int F_min = min_F;
max_F = max(max(F_max*nums[i],F_min*nums[i]),nums[i]);
min_F = min(min(F_min*nums[i],F_max*nums[i]),nums[i]);
ans = max(max_F,ans);
}
return ans;
}
};
|
这个题目时间复杂度极度好!!!
时间O(n) 空间O(1)
2020.05.19
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
示例 1:
输入: “aba”
输出: True
示例 2:
输入: “abca”
输出: True
解释: 你可以删除c字符。
这道题目 其实考点容易的
回文串 那么双指针查找就好了
但是如何判断去除一个字符之后还是回文串呢?
我一开始的想法是
如果 i j 两个指针的字符不一致,那么判断去除哪个字符
如何判断 假设 i+1和 j字符相同 那么去除 i字符
假设 i 和 j+1字符相同 那么去除j字符
如果上述都不成立 直接返回false。
但是出现了一个很尴尬的情况
cuppucu: 我们看的出来去除u字符,但是 按照判断逻辑
c+1 = u字符和 j的u字符相等 所以应该去除c字符。
这个时候我就有点难受了。。。。
下面是正确思路:
去除一个字符后 剩下的就应该是回文串 如果不是 那么就直接返回false
代码很好写
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
bool validPalindrome(string s) {
for(int i = 0, j = s.size()-1;i<j;i++,j--){
if(s[i]!=s[j]){
bool res1=true,res2=true;
for(int start = i+1,end =j;start<end;start++,end--){
if(s[start]!=s[end])
res1 = false;
}
for(int start = i,end =j-1;start<end;start++,end--){
if(s[start]!=s[end])
res2 = false;
}
if(res1||res2)
return true;
else
return false;
}
}
return true;
}
};
|
2020.05.22
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/
9 20
/
15 7
直接看题解好的吧!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class Solution {
private Map<Integer,Integer> indexmap;
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = inorder.length;
indexmap = new HashMap<Integer,Integer>();
for(int i=0;i<n;i++){
indexmap.put(inorder[i],i);
}
return liduoan_buildTree(preorder,inorder,0,n-1,0,n-1);
}
public TreeNode liduoan_buildTree(int[] preorder,int[] inorder,int preleft,int preright,int inorder_left,int inorder_right){
if(preleft>preright)
return null;
int pre_root = preleft;
int order_root = indexmap.get(preorder[preleft]);
TreeNode root = new TreeNode(preorder[pre_root]);
int size_left_tree = order_root - inorder_left;
root.left = liduoan_buildTree(preorder,inorder,preleft+1,preleft+size_left_tree,inorder_left,order_root-1);
root.right = liduoan_buildTree(preorder,inorder,preleft+size_left_tree+1,preright,order_root+1,inorder_right);
return root;
}
}
|
2020.05.23
难度困难513
给你一个字符串 S、一个字符串 T,请在字符串 S 里面找出:包含 T 所有字符的最小子串。
示例:
1
2
| 输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"
|
滑动窗口
维护一个窗口,不断滑动,然后更新答案。
算法的大致逻辑:
1
2
3
4
5
6
7
8
9
10
11
12
13
| int left = 0;
int right = 0;
while(right<s.size()){
windows.add(s[right]);
right++;
while(windows needs shrink){
windows.remove(s[left]);
left++;
}
}
|
这道题目的算法逻辑:
1、我们在s中使用左右指针技巧,初始化left=right=0,把索引左闭右开区间称为一个窗口
2、不断增加right来扩大窗口,直到符合字符串
3、停止增加right,然后增加left来缩小窗口
4、重复2、3步,直到s的尽头
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Solution {
public String minWindow(String s, String t) {
HashMap<Character,Integer> needs = new HashMap<>();
HashMap<Character,Integer> windows = new HashMap<>();
for(int i=0;i<t.length();i++){
char temp = t.charAt(i);
needs.put(temp,needs.getOrDefault(temp,0)+1);
}
int left=0,right=0,minLen=Integer.MAX_VALUE;
int count=0;
int start=0,end=0;
while(right<s.length()){
char temp = s.charAt(right);
if(needs.containsKey(temp)){
windows.put(temp,windows.getOrDefault(temp,0)+1);
if(windows.get(temp).compareTo(needs.get(temp))==0){
count++;
}
}
right++;
while(count==needs.size()){
if(right-left<minLen){
start = left;
end = right;
minLen = right-left;
}
char noneed = s.charAt(left);
if(needs.containsKey(noneed)){
windows.put(noneed,windows.get(noneed)-1);
if(windows.get(noneed).compareTo(needs.get(noneed))<0){
count--;
}
}
left++;
}
}
return minLen==Integer.MAX_VALUE? "":s.substring(start,end);
}
}
|